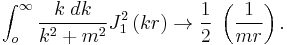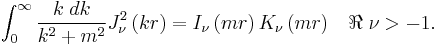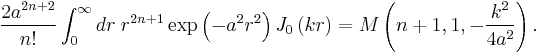Common integrals in quantum field theory
There are common integrals in quantum field theory that appear repeatedly.[1] These integrals are all variations and generalizations of gaussian integrals to the complex plane and to multiple dimensions. Other integrals can be approximated by versions of the gaussian integral. Fourier integrals are also considered.
Variations on a simple gaussian integral
Gaussian integral
The first integral, with broad application outside of quantum field theory, is the gaussian integral.
In physics the factor of 1/2 in the argument of the exponential is common.
Note:
Thus we obtain
Slight generalization of the gaussian integral
where we have scaled
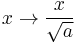 .
.
Integrals of exponents and even powers of x
and
In general
Note that the integrals of exponents and odd powers of x are 0, due to odd symmetry.
Integrals with a linear term in the argument of the exponent
This integral can be performed by completing the square.
Integrals with an imaginary linear term in the argument of the exponent
The integral
is proportional to the Fourier transform of the gaussian where  is the conjugate variable of
is the conjugate variable of  .
.
By again completing the square we see that the Fourier transform of a gaussian is also a gaussian, but in the conjugate variable. The larger  is, the narrower the gaussian in
is, the narrower the gaussian in  and the wider the gaussian in
and the wider the gaussian in  . This is a demonstration of the uncertainty principle.
. This is a demonstration of the uncertainty principle.
Integrals with a complex argument of the exponent
The integral of interest is (for an example of an application see Relation between Schrödinger's equation and the path integral formulation of quantum mechanics)
We assume that 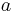 may be complex. All other quantities are real.
may be complex. All other quantities are real.
Completing the square
By analogy with the previous integrals
This result is valid as an integration in the complex plane as long as 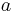 has a positive imaginary part.
has a positive imaginary part.
Gaussian integrals in higher dimensions
The one-dimensional integrals can be generalized to multiple dimensions.[2]
Here  is a real symmetric matrix.
is a real symmetric matrix.
This integral is performed by diagonalization of  with an orthogonal transformation
with an orthogonal transformation
where  is a diagonal matrix and
is a diagonal matrix and 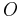 is an orthogonal matrix. This decouples the variables and allows the integration to be performed as
is an orthogonal matrix. This decouples the variables and allows the integration to be performed as 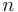 one-dimensional integrations.
one-dimensional integrations.
This is best illustrated with a two-dimensional example.
Example: Simple gaussian integration in two dimensions
The gaussian integral in two dimensions is
where  is a two-dimensional symmetric matrix with components specified as
is a two-dimensional symmetric matrix with components specified as
and we have used the Einstein summation convention.
Diagonalize the matrix
The first step is to diagonalize the matrix.[3] Note that
where, since A is a real symmetric matrix, we can choose 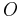 to be an orthogonal matrix, and hence also a unitary matrix.
to be an orthogonal matrix, and hence also a unitary matrix.
We choose 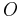 such that
such that
is diagonal.
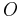 can be obtained from the eigenvectors of
can be obtained from the eigenvectors of  .
.
Eigenvalues of A
To find the eigenvectors of  one first finds the eigenvalues
one first finds the eigenvalues  of
of  given by
given by
![\bigl[ \begin{smallmatrix}
a&c\\ c&b
\end{smallmatrix} \bigr]
\bigl[ \begin{smallmatrix}
u\\ v
\end{smallmatrix} \bigr] =
\lambda \bigl[ \begin{smallmatrix}
u\\ v
\end{smallmatrix} \bigr]](/2012-wikipedia_en_all_nopic_01_2012/I/08cd28fc4c87b55c4b107401f2653b9a.png) .
.
The eigenvalues are solutions of the characteristic polynomial
which are
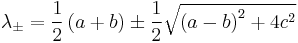 .
.
Eigenvectors of A
Substitution of the eigenvalues back into the eigenvector equation yields
or
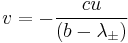 .
.
From the characteristic equation we know
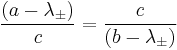 .
.
Also note
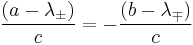 .
.
The eigenvectors can be written
and
for the two eigenvectors. Here 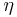 is a normalizing factor given by
is a normalizing factor given by
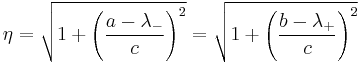 .
.
It is easily verified that the two eigenvectors are orthogonal to each other.
Construction of the orthogonal matrix
The orthogonal matrix is constructed by assigning the normalized eigenvectors as columns in the orthogonal matrix
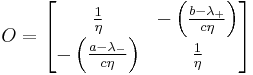 .
.
Note that the detrminant of O is equal to one.
If we define
then the orthogonal matrix can be written
which is simply a rotation of the eigenvectors.
The inverse is
Diagonal matrix
The diagonal matrix becomes
with eigenvectors
and
Numerical example
The eigenvalues are
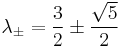 .
.
The eigenvectors are
and
where
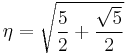 .
.
The orthogonal vector is
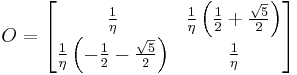 .
.
It is easily verified that the detrminant of O is 1.
The inverse of O is
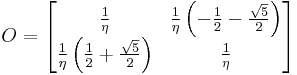 .
.
The diagonal matrix becomes
with the eigenvectors
and
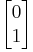 .
.
Rescale the variables and integrate
With the diagonalization the integral can be written
where
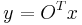 .
.
Since the coordinate transformation is simply a rotation of coordinates the Jacobian determinant of the transformation is one yielding
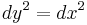 .
.
The integrations can now be performed.
which is the advertised solution.
Integrals with complex and linear terms in multiple dimensions
With the two-dimensional example it is now easy to see the generalization to the complex plane and to multiple dimensions.
Integrals with a linear term in the argument
Integrals with an imaginary linear term
Integrals with a complex quadratic term
Integrals with differential operators in the argument
As an example consider the integral[4]
where 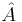 is a differential operator with
is a differential operator with  and
and  functions of spacetime, and
functions of spacetime, and 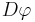 indicates integration over all possible paths. In analogy with the matrix version of this integral the solution is
indicates integration over all possible paths. In analogy with the matrix version of this integral the solution is
where
and 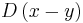 , called the propagator, is the inverse of
, called the propagator, is the inverse of 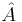 , and
, and 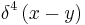 is the Dirac delta function.
is the Dirac delta function.
Similar arguments yield
and
![\int \exp\left[ i \int d^4x \left ( \frac 1 2 \varphi \hat A \varphi %2B J \varphi \right) \right ] D\varphi \; \propto \;
\exp \left( { i\over 2} \int d^4x \; d^4y J\left ( x \right ) D\left ( x - y \right ) J\left( y \right ) \right)](/2012-wikipedia_en_all_nopic_01_2012/I/d07a792846126656cc2834732b58f5d2.png) .
.
See Path-integral formulation of virtual-particle exchange for an application of this integral.
Integrals that can be approximated by the method of steepest descent
In quantum field theory n-dimensional integrals of the form
appear often. Here 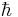 is the reduced Planck's constant and f is a function with a positive minimum at
is the reduced Planck's constant and f is a function with a positive minimum at 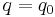 . These integrals can be approximated by the method of steepest descent.
. These integrals can be approximated by the method of steepest descent.
For small values of Planck's constant, f can be expanded about its minimum
![\int_{-\infty}^{\infty} \exp\left[ -{1 \over \hbar} \left( f\left( q_0 \right) %2B {1\over 2} \left( q-q_0\right)^2f^{\prime \prime} \left( q-q_0\right) %2B \cdots \right ) \right] d^nq](/2012-wikipedia_en_all_nopic_01_2012/I/b7f96b6c676e0430b6e08507ca19e91e.png) .
.
Here 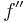 is the n by n matrix of second derivatives evaluated at the minimum of the function.
is the n by n matrix of second derivatives evaluated at the minimum of the function.
If we neglect higher order terms this integral can be integrated explicitly.
![\int_{-\infty}^{\infty} \exp\left[ -{1 \over \hbar} \left( f\left( q \right) \right ) \right] d^nq \approx
\exp\left[ -{1 \over \hbar} \left( f\left( q_0 \right) \right ) \right] \sqrt{ (2 \pi \hbar )^n \over \det f^{\prime \prime} }](/2012-wikipedia_en_all_nopic_01_2012/I/0254891ceab1b892b1c7b32b82c1a471.png) .
.
Integrals that can be approximated by the method of stationary phase
A common integral is a path integral of the form
where 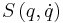 is the classical action and the integral is over all possible paths that a particle may take. In the limit of small
is the classical action and the integral is over all possible paths that a particle may take. In the limit of small 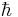 the integral can be evaluated in the stationary phase approximation. In this approximation the integral is over the path in which the action is a minimum. Therefore, this approximation recovers the classical limit of mechanics.
the integral can be evaluated in the stationary phase approximation. In this approximation the integral is over the path in which the action is a minimum. Therefore, this approximation recovers the classical limit of mechanics.
Fourier integrals
Dirac delta function
The Dirac delta function in spacetime can be written as a Fourier transform[5]
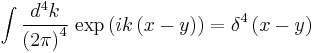 .
.
In general, for any dimension 
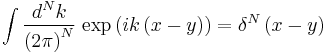 .
.
Fourier integrals of forms of the Coulomb potential
Laplacian of 1/r
While not an integral, the identity in three-dimensional Euclidean space
where
is a consequence of Gauss's theorem and can be used to derive integral identities. For an example see Longitudinal and transverse vector fields.
This identity implies that the Fourier integral representation of 1/r is
Yukawa Potential: The Coulomb potential with mass
The Yukawa potential in three dimensions can be represented as an integral over a Fourier transform[6]
where
and
See Static forces and virtual-particle exchange for an application of this integral.
In the small m limit the integral reduces to
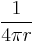 .
.
To derive this result note:
Modified Coulomb potential with mass
where the hat indicates a unit vector in three dimensional space.
In the small m limit the integral goes to zero.
To derive this result note:
where
Note that in the limit that
that
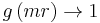 .
.
Longitudinal potential with mass
where the hat indicates a unit vector in three dimensional space.
In the small m limit the integral reduces to
To derive this result note:
where the cross terms vanish. The integral can be written
![=
{1\over 2} {e^{ - m r } \over 4 \pi r } \left[ \mathbf 1 - \mathbf{\hat r} \mathbf{\hat r} \right]
%2B
{e^{ - m r } \over 4 \pi r } \left\{ 1%2B {2\over mr }
- {2\over \left(mr\right)^2 } \left( e^{mr} -1 \right) \right \}
\left\{ {1\over 2} \left[\mathbf 1 %2B \mathbf{\hat r} \mathbf{\hat r}\right] \right\}](/2012-wikipedia_en_all_nopic_01_2012/I/3ce3b09d61e5881ecdcf45ce0774079d.png) .
.
Transverse potential with mass
In the small mr limit the integral goes to
For large distance, the integral falls off as the inverse cube of r
For applications of this integral see Darwin Lagrangian and Darwin interaction in a vacuum.
Angular integration in cylindrical coordinates
There are two important integrals. The angular integration of an exponential in cylindrical coordinates can be written in terms of Bessel functions of the first kind[7][8]
and
For applications of these integrals see Magnetic interaction between current loops in a simple plasma or electron gas.
Bessel functions
Integration of the cylindrical propagator with mass
First power of a Bessel function
See Abramowitz and Stegun.[9]
For 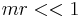 , we have[10]
, we have[10]
For an application of this integral see Two line charges embedded in a plasma or electron gas.
Square of Bessel Functions
The integration of the propagator in cylindrical coordinates is[11]
For small mr the integral becomes
For large mr the integral becomes
For applications of this integral see Magnetic interaction between current loops in a simple plasma or electron gas.
In general
Integration over a magnetic wave function
The two-dimensional integral over a magnetic wave function is[12]
Here, M is a confluent hypergeometric function. For an application of this integral see Charge density spread over a wave function.
References
- ^ A. Zee (2003). Quantum Field Theory in a Nutshell. Princeton University. ISBN 0-691-01019-6. pp. 13-15
- ^ Frederick W. Byron and Robert W. Fuller (1969). Mathematics of Classical and Quantum Physics. Addison-Wesley. ISBN 0-201-00746-2.
- ^ Herbert S. Wilf (1978). Mathematics for the Physical Sciences. Dover. ISBN 0-486-63635-6.
- ^ Zee, pp. 21-22.
- ^ Zee, p. 23.
- ^ Zee, p. 26, 29.
- ^ I. S. Gradshteyn and I. M. Ryzhik (1965). Tables of Integrals, Seies, and Products. Academic Press. ISBN 65-29097. p. 402
- ^ Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 047130932X. p. 113
- ^ M. Abramowitz and I. Stegun (1965). Handbook of Mathematical Functions. Dover. ISBN 486-61272-4. Section 11.4.44
- ^ Jackson, p. 116
- ^ I. S. Gradshteyn and I. M. Ryzhik, p. 679
- ^ Abramowitz and Stegun, Section 11.4.28
See also
|
|||||
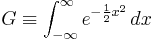
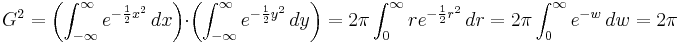
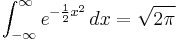
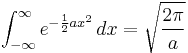
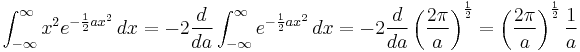
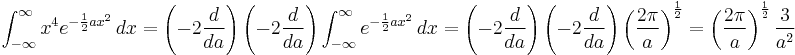
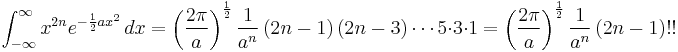
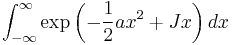
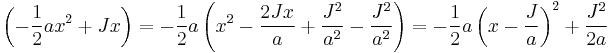
![\int_{-\infty}^{\infty} \exp\left( -{1 \over 2} a x^2 %2B Jx\right ) dx = \exp\left( { J^2 \over 2a } \right ) \int_{-\infty}^{\infty} \exp \left [ -{1 \over 2} a \left ( x - { J \over a } \right )^2 \right ] dx = \exp\left( { J^2 \over 2a } \right )\int_{-\infty}^{\infty} \exp\left( -{1 \over 2} a x^2 \right ) dx = \left ( {2\pi \over a } \right ) ^{1\over 2} \exp\left( { J^2 \over 2a }\right )](/2012-wikipedia_en_all_nopic_01_2012/I/7d40d914d1b783295b92e9748bc7f2ac.png)
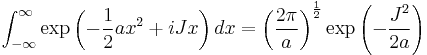
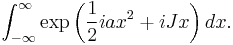
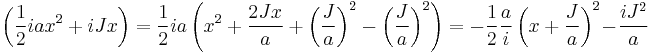
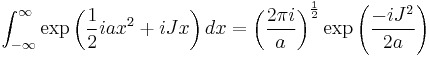
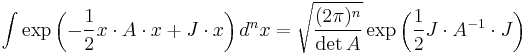
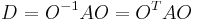
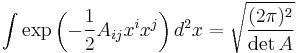
![A = \bigl[ \begin{smallmatrix}
a&c\\ c&b
\end{smallmatrix} \bigr]](/2012-wikipedia_en_all_nopic_01_2012/I/f8847673fbb98989bdf3a9ff981190a3.png)
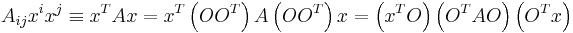
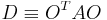
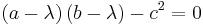
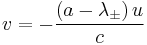
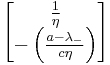
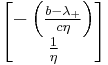
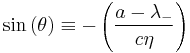
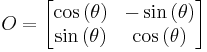
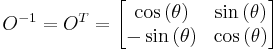
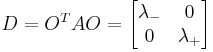
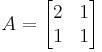
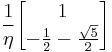
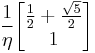
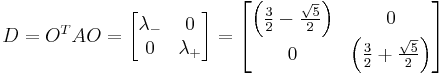
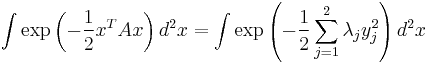
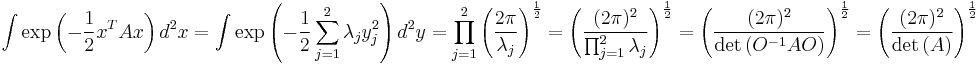
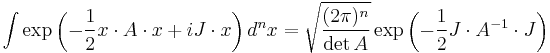
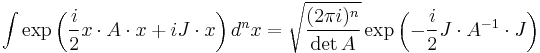
![\int \exp\left[ \int d^4x \left ( -\frac 1 2 \varphi \hat A \varphi %2B J \varphi \right) \right ] D\varphi](/2012-wikipedia_en_all_nopic_01_2012/I/e0b176578d63600fbf6304ad21dab972.png)
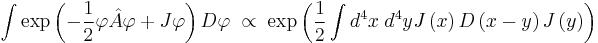
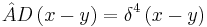
![\int \exp\left[ \int d^4x \left ( -\frac 1 2 \varphi \hat A \varphi %2B i J \varphi \right) \right ] D\varphi \; \propto \;
\exp \left( - { 1\over 2} \int d^4x \; d^4y J\left ( x \right ) D\left ( x - y \right ) J\left( y \right ) \right)](/2012-wikipedia_en_all_nopic_01_2012/I/5bda247086c31a7c69e12505a239f788.png)
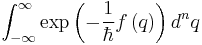
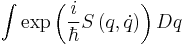
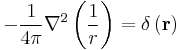
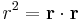
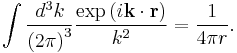
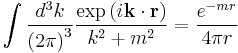
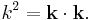
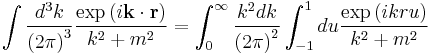
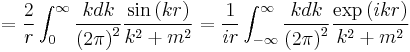
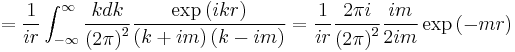
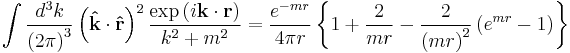
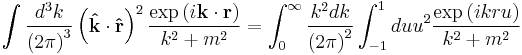
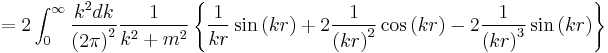
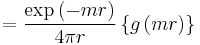
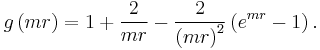
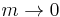
![\int { d^3 k \over \left ( 2 \pi \right ) ^3 }
\; \mathbf{\hat k} \mathbf{\hat k} \;
{ \exp \left ( i\mathbf \mathbf k \cdot \mathbf r \right ) \over k^2 %2Bm^2 }
=
{1\over 2} {e^{ - m r } \over 4 \pi r } \left[ \mathbf 1 - \mathbf{\hat r} \mathbf{\hat r} \right]
%2B
{1\over 2} {e^{ - m r } \over 4 \pi r } \left\{ 1%2B {2\over mr}
- {2 \over \left( mr \right)^2 } \left( e^{mr} -1 \right) \right \}
\left[\mathbf 1 %2B \mathbf{\hat r} \mathbf{\hat r}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/9a8ed24bb29ec2c650b92ec1641b59f1.png)
![{1\over 2} {1 \over 4 \pi r } \left[ \mathbf 1 - \mathbf{\hat r} \mathbf{\hat r} \right] .](/2012-wikipedia_en_all_nopic_01_2012/I/cc34b19f46af87b586fa1b8273ab8694.png)
![\int { d^3 k \over \left ( 2 \pi \right ) ^3 } \mathbf{\hat k} \mathbf{\hat k}
{ \exp \left ( i\mathbf k \cdot \mathbf r \right ) \over k^2 %2Bm^2 }
=
\int { d^3 k \over \left ( 2 \pi \right ) ^3 }
\left[
\left( \mathbf{\hat k}\cdot \mathbf{\hat r}\right)^2\mathbf{\hat r} \mathbf{\hat r}
%2B \left( \mathbf{\hat k}\cdot \mathbf{\hat \theta}\right)^2\mathbf{\hat \theta} \mathbf{\hat \theta}
%2B \left( \mathbf{\hat k}\cdot \mathbf{\hat \phi}\right)^2\mathbf{\hat \phi} \mathbf{\hat \phi}
\right]
{ \exp \left ( i\mathbf k \cdot \mathbf r \right ) \over k^2 %2Bm^2 }](/2012-wikipedia_en_all_nopic_01_2012/I/eb8eec0a96a68f5dfc2bcde6776a4981.png)
![=
{1 \over 4 \pi r } \exp \left ( - m r \right ) \left\{ 1%2B {2\over mr }
- {2\over \left(mr\right)^2 } \left( e^{mr} -1 \right) \right \}
\left\{\mathbf 1 - {1\over 2} \left[\mathbf 1 - \mathbf{\hat r} \mathbf{\hat r}\right] \right\}
%2B
\int_0^{\infty} {k^2 dk \over \left ( 2 \pi \right )^2 } \int_{-1}^{1} du {\exp\left( ikru \right) \over k^2 %2B m^2}
{1\over 2} \left[ \mathbf 1 - \mathbf{\hat r} \mathbf{\hat r} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/80767ce06f72d88b3bf3f5f0853c8074.png)
![\int { d^3 k \over \left ( 2 \pi \right ) ^3 }
\; \left[ \mathbf 1 - \mathbf{\hat k} \mathbf{\hat k} \right] \;
{ \exp \left ( i\mathbf \mathbf k \cdot \mathbf r \right ) \over k^2 %2Bm^2 }
=
{1\over 2} {e^{ - m r } \over 4 \pi r } \left\{
{2 \over \left( mr \right)^2 } \left( e^{mr} -1 \right) - {2\over mr} \right \}
\left[\mathbf 1 %2B \mathbf{\hat r} \mathbf{\hat r}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/71782edf3d9c16d104b6d411ec295afa.png)
![{1\over 2} {1 \over 4 \pi r }
\left[\mathbf 1 %2B \mathbf{\hat r} \mathbf{\hat r}\right]
.](/2012-wikipedia_en_all_nopic_01_2012/I/578090559934178a1905b197c44f31e7.png)
![{1\over 4 \pi m^2r^3 }
\left[\mathbf 1 %2B \mathbf{\hat r} \mathbf{\hat r}\right]
.](/2012-wikipedia_en_all_nopic_01_2012/I/de349c2e190e1f31bbd1e303fa124530.png)
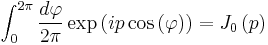
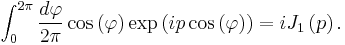
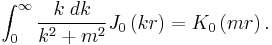
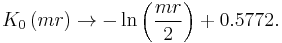
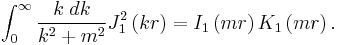
![\int_o^{\infty} {k\; dk \over k^2 %2Bm^2} J_1^2 \left( kr \right)
\rightarrow
{1\over 2 }\left[ 1 - {1\over 8} \left(mr\right)^2 \right]
.](/2012-wikipedia_en_all_nopic_01_2012/I/a70cd7cc68408f861a91d7e8ba07b3b4.png)